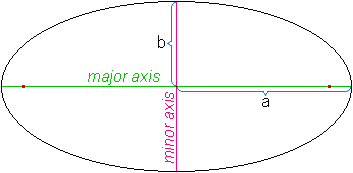
The semimajor axis is half of the major axis in an ellipse at its longest diameter, a line running through its center and the foci. The semimajor axis runs from the center to the ellipse’s edge through a focus. It is that measure of the orbit’s radius at its most distant points. In the case of a circle, it then becomes the radius itself. We can think of it as any ellipse’s long radius.
In the world of astronomy, the semimajor axis is known to be part of an orbit. For objects within the solar system, this axis is directly related to the orbital periods, which is noted in Kepler’s third law.
A celestial body’s orbiting path all around the barycentre is a classic example of an ellipse. So is the path relative to the primary body, or host. The semimajor axis employed in astronomy will always be that distance from the primary body to the secondary, or orbiting body. This means that the orbital parameters of both bodies are expressed in heliocentric terms.
Looking alone at the Earth-moon system, this depicts the difference between orbit examples, the primo centric and absolute orbits, with the mass ratio at 81.30059. With this particular distance characteristic, the geocentric lunar orbit presents a semimajor axis of about 384,400 kilometers. On the other hand, the barycentric lunar orbit reports an axis of 379,700 kilometers. These values can be reliably expressed with using geocentric semimajor axis values.