A neutrino is a little-understood, mysterious particle smaller than an atom. It is considered as one of the most important particles that our world is composed of. Neutrinos have only been recently discovered (or deduced to exist). They are thought of as similar to electrons, except that they don’t carry an electric charge. Because they are neutral, they were named neutrinos from the Italian which means “little neutral one.” Neutral particles like neutrinos are not affected by electromagnetic forces.
The study of subatomic particles like neutrinos normally lie within the realm of physics, but it is in astronomy that scientists are able to study neutrinos in action. For example, in 1968, an experiment was able to detect neutrinos produced by the burning gases on the sun’s surface. And in 1987, a burst of neutrinos was detected from the explosion of a supernova.
This 1987 event marked the “official” beginning of a branch of science called neutrino astronomy: a kind of a marriage between physics and astronomy whose main objective is to shed light on the nature and characteristics of neutrinos.
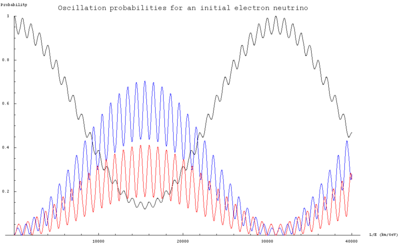
So far, three types of neutrinos have been discovered: the electron-neutrino, the tau-neutrino and the muon-neutrino. They, together with electrons, are classified as leptons. Leptons and quarks— collectively known as Fermions—are the fundamental building blocks of the universe.
Understanding Neutrinos